DEFINICIONES
En términos matemáticos, un árbol es cualquier conjunto de puntos, llamados vértices, y cualquier conjunto de pares de distintos vértices, llamados lados o ramas, tales que:
· Hay una secuencia de ramas, llamada paso de cualquier vértice a cualquier otro vértice.
· No hay lazos, o sea, que no hay pasos que comiencen en un vértice y puedan volver al mismo vértice.
Los árboles que tienen un vértice o nodo especial, llamado raíz, reciben el nombre de árboles enraizados. La particularidad del nodo raíz es que no puede ser hijo de otro nodo.
Un árbol es una estructura de datos no lineal. Las estructuras de datos lineales se caracterizan por que a cada elemento le corresponde no más que un elemento siguiente. En las estructuras de datos no lineales, como el árbol, un elemento puede tener diferentes " siguientes elementos ", introduciendo una estructura de bifurcación, también conocidas como estructuras multi enlazada.
Un árbol ordenado se define como un árbol en el que los subárboles de cada nodo forman un conjunto ordenado. En una árbol ordenado podemos hablar del primero, segundo o último hijo de un nodo particular. El primer hijo de un nodo, en un árbol ordenado, se denomina con frecuencia el hijo más viejo de este nodo y el último hijo, se denomina el hijo más joven.
USOS
Veamos algunos ejemplos donde la estructura de datos árbol puede ser muy util :
- Los sistemas de archivos de los sistemas operativos, compuestos por jerarquías de directorios y archivos.
- La jerarquía de clases en los lenguajes orientados a objetos.
- La jerarquía de países, provincias, departamentos y municipios que organiza al poder político de una república.
Tipos de arboles
- Arboles binarios
- árbol multicamino
Árbol binario
Un árbol binario es una estructura de datos en la cual cada nodo siempre tiene un hijo izquierdo y un hijo derecho. No pueden tener más de dos hijos (de ahí el nombre "binario"). Si algún hijo tiene como referencia a null, es decir que no almacena ningún dato, entonces este es llamado un nodo externo. En el caso contrario el hijo es llamado un nodo interno. Usos comunes de los árboles binarios son los árboles binarios de búsqueda, los montículos binarios y Codificación de Huffman.
árbol multicamino
Un árbol multicamino posee un grado g mayor a dos, donde cada nodo de información del árbol tiene un máximo de g hijos.
Sea un árbol de m-caminos A, es un árbol m-caminos si y solo si:
- A está vacío
Existen muchas aplicaciones en las que el volumen de la información es tal, que los datos no caben en la memoria principal y es necesario almacenarlos, organizados en archivos, en dispositivos de almacenamiento secundario. Esta organización de archivos debe ser suficientemente adecuada como para recuperar los datos del mismo en forma eficiente.
RECORRIDO
Hay tres manera de recorrer un árbol : en inorden, preorden y postorden. Cada una de ellas tiene una secuencia distinta para analizar el árbol como se puede ver a continuación:
- INORDEN
- Recorrer el subarbol izquierdo en inorden.
- Examinar la raíz.
- Recorrer el subarbol derecho en inorden.
- PREORDEN
- Examinar la raíz.
- Recorrer el subarbol izquierdo en preorden.
- recorrer el subarbol derecho en preorden.
- POSTORDEN
- Recorrer el subarbol izquierdo en postorden.
- Recorrer el subarbol derecho en postorden.
- Examinar la raíz.
PROGRAMA CLASE
package javaapplication3;
import java.awt.*;
import java.awt.event.*;
import javax.swing.*;
import javax.swing.tree.*;
import java.util.*;
public class SimpleTree
{ public static void main(String[] args)
{ JFrame frame = new SimpleTreeFrame();
frame.show();
}
}
class SimpleTreeFrame extends JFrame
{
DefaultMutableTreeNode root = new DefaultMutableTreeNode("Mundo");
DefaultMutableTreeNode arge = new DefaultMutableTreeNode("Argentina");
DefaultMutableTreeNode sant = new DefaultMutableTreeNode("Santa Fe");
DefaultMutableTreeNode rafa = new DefaultMutableTreeNode("Rafaela");
DefaultMutableTreeNode rosa = new DefaultMutableTreeNode("Rosario");
DefaultMutableTreeNode safe = new DefaultMutableTreeNode("Santa Fe");
DefaultMutableTreeNode vena = new DefaultMutableTreeNode("Venado Tuerto");
DefaultMutableTreeNode vill = new DefaultMutableTreeNode("Villa Constitucion");
DefaultMutableTreeNode cord = new DefaultMutableTreeNode("Cordoba");
DefaultMutableTreeNode codo = new DefaultMutableTreeNode("Cordoba");
DefaultMutableTreeNode cbro = new DefaultMutableTreeNode("Cura Brochero");
DefaultMutableTreeNode rcua = new DefaultMutableTreeNode("Rio Cuarto");
DefaultMutableTreeNode chac = new DefaultMutableTreeNode("Chaco");
DefaultMutableTreeNode resi = new DefaultMutableTreeNode("Resistencia");
DefaultMutableTreeNode vang = new DefaultMutableTreeNode("Villa Angela");
DefaultMutableTreeNode chil = new DefaultMutableTreeNode("Chile");
DefaultMutableTreeNode regi = new DefaultMutableTreeNode("Region Metropolitana");
DefaultMutableTreeNode schi = new DefaultMutableTreeNode("Santiago de Chile");
public SimpleTreeFrame()
{ setTitle("SimpleTree");
setSize(300, 200);
addWindowListener(new WindowAdapter()
{ public void windowClosing(WindowEvent e)
{ System.exit(0);
}
} );
root.add(arge); // Enlazado de nodos
arge.add(sant); // Enlazado de nodos
sant.add(rafa); // Enlazado de nodos
sant.add(rosa); // Enlazado de nodos
sant.add(safe); // Enlazado de nodos
sant.add(vena); // Enlazado de nodos
sant.add(vill); // Enlazado de nodos
arge.add(cord); // Enlazado de nodos
cord.add(codo); // Enlazado de nodos
cord.add(cbro); // Enlazado de nodos
cord.add(rcua); // Enlazado de nodos
arge.add(chac); // Enlazado de nodos
chac.add(resi); // Enlazado de nodos
chac.add(vang); // Enlazado de nodos
root.add(chil); // Enlazado de nodos
chil.add(regi); // Enlazado de nodos
regi.add(schi); // Enlazado de nodos
JTree tree = new JTree(root);
Container contentPane = getContentPane();
contentPane.add(new JScrollPane(tree));
Enumeration hijos = sant.children(); // Enumeracion de hijos
while ( hijos.hasMoreElements() ) // Enumeracion de hijos
{ // Enumeracion de hijos
System.err.println("Hijos de Santa Fe : "+hijos.nextElement()); // Enumeracion de hijos
} // Enumeracion de hijos
boolean hoja = vena.isLeaf(); // Consulta Hoja
System.err.println("Es Venado Tuerto hoja : "+hoja); // Consulta Hoja
Enumeration breadth = root.breadthFirstEnumeration(); // Enumeracion Nodos
while ( breadth.hasMoreElements() ) // Enumeracion Nodos
{ // Enumeracion Nodos
System.err.println("Breadth First : "+breadth.nextElement()); // Enumeracion Nodos
} // Enumeracion Nodos
Enumeration depth = root.depthFirstEnumeration(); // Enumeracion Nodos
while ( depth.hasMoreElements() ) // Enumeracion Nodos
{ // Enumeracion Nodos
System.err.println("Depth First : "+depth.nextElement()); // Enumeracion Nodos
} // Enumeracion Nodos
Enumeration preorder = root.preorderEnumeration(); // Enumeracion Nodos
while ( preorder.hasMoreElements() ) // Enumeracion Nodos
{ // Enumeracion Nodos
System.err.println("Pre Order : "+preorder.nextElement()); // Enumeracion Nodos
} // Enumeracion Nodos
Enumeration postorder = root.postorderEnumeration(); // Enumeracion Nodos
while ( postorder.hasMoreElements() ) // Enumeracion Nodos
{ // Enumeracion Nodos
System.err.println("Post Order : "+postorder.nextElement()); // Enumeracion Nodos
} // Enumeracion Nodos
}
}
import java.awt.*;
import java.awt.event.*;
import javax.swing.*;
import javax.swing.tree.*;
import java.util.*;
public class SimpleTree
{ public static void main(String[] args)
{ JFrame frame = new SimpleTreeFrame();
frame.show();
}
}
class SimpleTreeFrame extends JFrame
{
DefaultMutableTreeNode root = new DefaultMutableTreeNode("Mundo");
DefaultMutableTreeNode arge = new DefaultMutableTreeNode("Argentina");
DefaultMutableTreeNode sant = new DefaultMutableTreeNode("Santa Fe");
DefaultMutableTreeNode rafa = new DefaultMutableTreeNode("Rafaela");
DefaultMutableTreeNode rosa = new DefaultMutableTreeNode("Rosario");
DefaultMutableTreeNode safe = new DefaultMutableTreeNode("Santa Fe");
DefaultMutableTreeNode vena = new DefaultMutableTreeNode("Venado Tuerto");
DefaultMutableTreeNode vill = new DefaultMutableTreeNode("Villa Constitucion");
DefaultMutableTreeNode cord = new DefaultMutableTreeNode("Cordoba");
DefaultMutableTreeNode codo = new DefaultMutableTreeNode("Cordoba");
DefaultMutableTreeNode cbro = new DefaultMutableTreeNode("Cura Brochero");
DefaultMutableTreeNode rcua = new DefaultMutableTreeNode("Rio Cuarto");
DefaultMutableTreeNode chac = new DefaultMutableTreeNode("Chaco");
DefaultMutableTreeNode resi = new DefaultMutableTreeNode("Resistencia");
DefaultMutableTreeNode vang = new DefaultMutableTreeNode("Villa Angela");
DefaultMutableTreeNode chil = new DefaultMutableTreeNode("Chile");
DefaultMutableTreeNode regi = new DefaultMutableTreeNode("Region Metropolitana");
DefaultMutableTreeNode schi = new DefaultMutableTreeNode("Santiago de Chile");
public SimpleTreeFrame()
{ setTitle("SimpleTree");
setSize(300, 200);
addWindowListener(new WindowAdapter()
{ public void windowClosing(WindowEvent e)
{ System.exit(0);
}
} );
root.add(arge); // Enlazado de nodos
arge.add(sant); // Enlazado de nodos
sant.add(rafa); // Enlazado de nodos
sant.add(rosa); // Enlazado de nodos
sant.add(safe); // Enlazado de nodos
sant.add(vena); // Enlazado de nodos
sant.add(vill); // Enlazado de nodos
arge.add(cord); // Enlazado de nodos
cord.add(codo); // Enlazado de nodos
cord.add(cbro); // Enlazado de nodos
cord.add(rcua); // Enlazado de nodos
arge.add(chac); // Enlazado de nodos
chac.add(resi); // Enlazado de nodos
chac.add(vang); // Enlazado de nodos
root.add(chil); // Enlazado de nodos
chil.add(regi); // Enlazado de nodos
regi.add(schi); // Enlazado de nodos
JTree tree = new JTree(root);
Container contentPane = getContentPane();
contentPane.add(new JScrollPane(tree));
Enumeration hijos = sant.children(); // Enumeracion de hijos
while ( hijos.hasMoreElements() ) // Enumeracion de hijos
{ // Enumeracion de hijos
System.err.println("Hijos de Santa Fe : "+hijos.nextElement()); // Enumeracion de hijos
} // Enumeracion de hijos
boolean hoja = vena.isLeaf(); // Consulta Hoja
System.err.println("Es Venado Tuerto hoja : "+hoja); // Consulta Hoja
Enumeration breadth = root.breadthFirstEnumeration(); // Enumeracion Nodos
while ( breadth.hasMoreElements() ) // Enumeracion Nodos
{ // Enumeracion Nodos
System.err.println("Breadth First : "+breadth.nextElement()); // Enumeracion Nodos
} // Enumeracion Nodos
Enumeration depth = root.depthFirstEnumeration(); // Enumeracion Nodos
while ( depth.hasMoreElements() ) // Enumeracion Nodos
{ // Enumeracion Nodos
System.err.println("Depth First : "+depth.nextElement()); // Enumeracion Nodos
} // Enumeracion Nodos
Enumeration preorder = root.preorderEnumeration(); // Enumeracion Nodos
while ( preorder.hasMoreElements() ) // Enumeracion Nodos
{ // Enumeracion Nodos
System.err.println("Pre Order : "+preorder.nextElement()); // Enumeracion Nodos
} // Enumeracion Nodos
Enumeration postorder = root.postorderEnumeration(); // Enumeracion Nodos
while ( postorder.hasMoreElements() ) // Enumeracion Nodos
{ // Enumeracion Nodos
System.err.println("Post Order : "+postorder.nextElement()); // Enumeracion Nodos
} // Enumeracion Nodos
}
}
PROGRAMA
void insertar(int nodo, int dato){
2 if(clave[nodo]>dato){
3 if(izq[nodo]==1)
{
4 izq[nodo]=crear_nodo(dato);
5 }else{
6 insertar(izq[nodo], dato);
7 }
8 }else{
9 if(der[nodo]==1){
10 der[nodo]=crear_nodo(dato);
11 }else{
12 insertar(der[nodo], dato);
13 }
14 }
15 }
GRAFOS
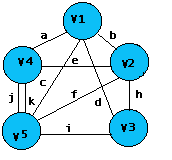
Un grafo, G, es un par ordenado de V y A, donde V es el conjunto de vértices o nodos del grafo y A es un conjunto de pares de vértices, a estos también se les llama arcos o ejes del grafo. Un vértice puede tener 0 o más aristas, pero toda arista debe unir exactamente a dos vértices.La notación G = A (V, A) se utiliza comúnmente para identificar un grafo.
ALGUNOS DE LOS PRINCIPALES TIPOS DE GRAFOS SON LOS QUE SE MUESTRAN A CONTINUACIÓN:
· Grafo regular: Aquel con el mismo grado en todos los vértices. Si ese grado es k lo llamaremos k-regular.
Por ejemplo, el primero de los siguientes grafos es 3-regular, el segundo es 2-regular y el tercero no es regular· Grafo bipartito: Es aquel con cuyos vértices pueden formarse dos conjuntos disjuntos de modo que no haya adyacencias entre vértices pertenecientes al mismo conjunto
Ejemplo.- de los dos grafos siguientes el primero es bipartito y el segundo no lo es· Grafo completo: Aquel con una arista entre cada par de vértices. Un grafo completo con n vértices se denota Kn.
A continuación pueden verse los dibujos de K3, K4, K5 y K6· Un grafo bipartito regular: se denota Km,n donde m, n es el grado de cada conjunto disjunto de vértices.
Aristas
Son las líneas con las que se unen las aristas de un grafo y con la que se construyen también caminos.
Si la arista carece de dirección se denota indistintamente {a, b} o {b, a}, siendo a y b los vértices que une.
Si {a ,b} es una arista, a los vértices a y b se les llama sus extremos.
- Aristas Adyacentes: Se dice que dos aristas son adyacentes si convergen en el mismo vértice.
- Aristas Paralelas: Se dice que dos aristas son paralelas si vértice inicial y el final son el mismo.
- Aristas Cíclicas: Arista que parte de un vértice para entrar en el mismo.
- Cruce: Son dos aristas que cruzan en un punto.
VÉRTICES
Son los puntos o nodos con los que esta conformado un grafo.
Llamaremos grado de un vértice al número de aristas de las que es extremo. Se dice que un vértice es `par' o `impar' según lo sea su grado.
· Vértices Adyacentes: si tenemos un par de vértices de un grafo (U, V) y si tenemos un arista que los une, entonces U y V son vértices adyacentes y se dice que U es el vértice inicial y V el vértice adyacente.
· Vértice Aislado: Es un vértice de grado cero.
· Vértice Terminal: Es un vértice de grado 1.
CAMINOS
Sean x, y " V, se dice que hay un camino en G de x a y si existe una sucesión finita no vacía de aristas {x,v1}, {v1,v2},..., {vn,y}. En este caso
· x e y se llaman los extremos del camino
· El número de aristas del camino se llama la longitud del camino.
· Si los vértices no se repiten el camino se dice propio o simple.
· Si hay un camino no simple entre 2 vértices, también habrá un camino simple entre ellos.
· Cuando los dos extremos de un camino son iguales, el camino se llama circuito o camino cerrado.
· Llamaremos ciclo a un circuito simple
· Un vértice a se dice accesible desde el vértice b si existe un camino entre ellos. Todo vértice es accesible respecto a si mismo
LAS APLICACIONES MÁS IMPORTANTES DE LOS GRAFOS SON LAS SIGUIENTES:
· Rutas entre ciudades.
· Determinar tiempos máximos y mínimos en un proceso.
· Flujo y control en un programa.
ARCOS
Los arcos se utilizan para representar relaciones entre estos objetos.